Links:

Melt Viscosity of Particle-Reinforced Polymers

The effect of fillers on the viscoelastic properties of polymer melts depends on the particle size and shape. In the case of submicroscopic particles, the particle surface chemistry and polymer composition also plays an important role. Often dispersants like fatty acid salts are added which coat the particles and overcome the propensity of the particles to agglomerate. Poor dispersion will not only increase the viscosity but will also affect the performance nad processing properties. To achieve the optimal properties, the filler particles have to be evenly dispersed in the polymer matrix.

At low particle concentrations, the effect of dispersed fillers on the viscosity is rather small. The increase in viscosity results mainly from the distortion of the flow lines of the continuous phase around the filler particles which leads to additional internal friction and energy dissipation. The smallest disturbance of the hydrodynamic flow field is caused by smooth spherical particles, while particles of irregular shape and rough surface cause a much greater disturbance. An exception are fibers which align themselves in the direction of the mass flow.

The flow behavior of very dilute polymer suspensions as a function of volume fraction of rigid spherical particles can be described with Einstein's equation of viscosity:⁵

η = η_m (1 + 5/2 φ_f)

where φ_f is the filler volume fraction and η_m is the viscosity of the polymer melt without filler. This equation, however, is only applicable to very dilute dispersions where particle-particle interaction and other surface effects like polymer-particle bridging can be neglected. To account for these interaction, a third term has to be added to the Einstein equation:⁶

η = η_m (1 + 5/2 φ_f + k_H φ_f²)

where k_H is the Huggins coefficient. This parameter is a measure for interparticle interaction.¹ In the case of repulsive spherical particles, k_H has a value of about 6.2² (Batchelor 1977). A similar power series might be applied to non-spherical particles:

η = η_m (1 + 5/2 φ_f + a₁ φ_f² + a₂ φ_f³ +...)

Polymers with a molecular weight below the critical entanglement weight show often quasi-Newtonian behavior at low shear rates. The viscosity of such filler- liquid systems can be described with the Maron-Pierce equation (1956):³

η_rel = η / η_m = (1 - φ_f / φ_m)^-2

where φ_m is the maximum volume fraction at which flow is possible.⁷ For repulsive particle-particle interaction the value of φ_m should be close to the maximum packing density (≈ 0.638) and for attractive interaction, φ_m is the value at which the suspension reaches its percolation threshold. The exact value of φ_m can be determined from a plot of square root of relative viscosity versus filler volume  fraction.

 

 

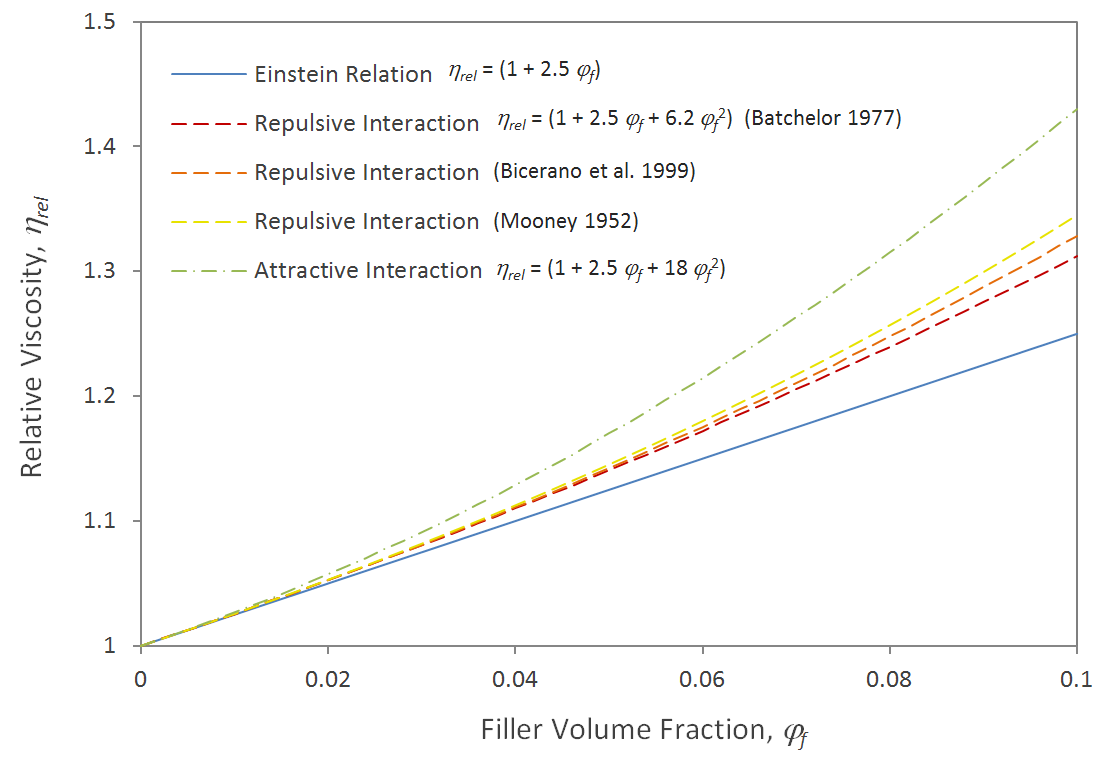
Bicerano et al. (1999) extended this equation to semi- and concentrated dispersions:¹

η_rel ≈ (1 - φ_f / φ_m)^-2 · [1 - 0.4 (φ_f / φ_m) + 0.34 (φ_f / φ_m)²)]

Accoording to Bicerano et al., this equation is accurate in many applications for both the dilute and concentrated regime.

Another popular semi-empirical equation was proposed by Mooney (1952).⁴

η_rel = exp[2.5φ_f / (1 - φ_f /φ_m)]

This equation can be written as a power series which can be approximated to Einstein's equation at very low concentrations.

As can be seen in the figure above, the effect of particle-particle interacion can be neglected below a filler volume fraction of about 0.2 (dilute dispersions). Below this loading, all four models give similar predictions.